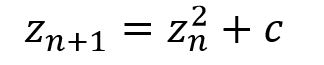前言

数学之美，人人皆知。今天我们就来看看数学是怎样影响图形绘制效果的吧。我们采用Julia集作为绘制对象，展示一下数学框架下的优美图形。

 

1 基本理论

Julia集是在复平面上形成分形的点的集合。简单来说，我们可以通过一个方程的迭代来确定复平面上的哪些点属于Julia集合。

常数c是我们预定义的复数常量，z是复平面上的一个点。如果经过一定次数的迭代计算，z的模仍然在一定范围内，则认为该点是收敛的，属于Julia集；否则认为发散，不属于Julia集。通常c的取值会影响Julia集的形状。例如，我们定义c= -0.8+0.156i，我们就能绘制出类似下图的形状。

2 实现方法

首先建立Unity工程，建立scene，创建一个材质叫做DrawingMat.mat，创建一个Shader文件叫做Drawing.shader，创建一个脚本叫做Drawing.cs，并挂载到场景中的摄像机上。Drawing.cs有一个公有变量mat，需要与DrawingMat.mat绑定，而DrawingMat.mat的shader就使用我们创建的Drawing.shader。

 

Drawing.cs源代码如下：

using UnityEngine;using System.Collections;[ExecuteInEditMode]public class Drawing : MonoBehaviour {	public Material mat;	void Start () {	}	void Update () {	}	void OnRenderImage(RenderTexture src, RenderTexture dest) {		Graphics.Blit(src, dest, mat);	}}

Drawing.shader源代码如下：

Shader "Custom/Drawing" {      Properties      {          //定义基本属性，可以从编辑器里面进行设置的变量          _MainTex ("Texture", 2D) = "white" {}         cx("cx",range(-0.8,0.375))=-0.8          cy("cy",range(-1,1))=0.156               scale("scale",range(1,3))=1.6    }      SubShader      {          Tags { "RenderType"="Opaque" }          LOD 100          Pass          {              CGPROGRAM              #pragma vertex vert              #pragma fragment frag              #include "UnityCG.cginc"              struct appdata              {                  float4 vertex : POSITION;                  float2 uv : TEXCOORD0;              };              struct v2f              {                  float2 uv : TEXCOORD0;                  float4 vertex : SV_POSITION;              };              sampler2D _MainTex;              float4 _MainTex_ST;             float cx ; //复数c的实部		    float cy ; //复数c的虚部            float scale;                           v2f vert (appdata v)              {                  v2f o;                  o.vertex = mul(UNITY_MATRIX_MVP,v.vertex);                  o.uv = v.uv.xy * _MainTex_ST.xy + _MainTex_ST.zw;                  return o;              }                         fixed4 frag (v2f i) : SV_Target              {  		        float ax = scale*(0.5-i.uv.x)/0.5;  //迭代初始值的实部		        float ay = scale*(0.5-i.uv.y)/0.5;  //迭代初始值的虚部		        float juliaValue;		        //进行200次迭代		        for(int index=0;index<200;index++)		        {		        	//迭代函数实现，先计算复数乘法，然后加上c		        	float _ax = ax*ax-ay*ay;		            float _ay = ay*ax+ax*ay;		            ax = _ax+cx;		            ay = _ay+cy;		            //计算模长，超过阈值则认为不属于Julia集，返回黑色		            juliaValue = sqrt(ax*ax+ay*ay);		            if(juliaValue > 100)		            {		            	return fixed4(0,0,0,1);		            }		        }   		        //Julia集内部的点，需要根据Julia值来计算颜色，这个可以自己设置颜色                return fixed4(juliaValue,(fixed)(sin(_Time*100)+1)/2,(fixed)(cos(_Time*50)+1)/2,1);              }              ENDCG          }      }  }

最终效果如下：